top of page

Aryabhata - 476AD

arya%20cover_edited.jpg

Aryabhatta is probably one of the only ancient Indian mathematicians whom you might know the name of. He's usually known for 'discovering' the number 0. A huge understatement regarding the vast amount of work done by him.

 

Aryabhata was an astronomer and mathematician in 476 AD with his work having an influence on the development of Islamic astronomy and is known to be referenced by other large Indian mathematicians such as Bhaskara II and Brahmagupta. In his first book, Ganita, he gave the names of the first 10 decimal places which is the foundation of the place value system which we still use today. Without this guy, we would most probably still be writing the number of times we cried over maths like this LXXXVIII

 

He also gives the algorithms for obtaining square and cubic roots using the decimal number system. Then he states an approximation for the value of π using the example of 62,832/20,000 (=3.1416) like no big deal. Which he states here:

 

caturadhikaṃ śatamaṣṭaguṇaṃ dvāṣaṣṭistathā sahasrāṇām

ayutadvayaviṣkambhasyāsanno vṛttapariṇāhaḥ.

Then he develops properties of similar right-angled triangles and two intersection circles. Further, he uses his version of the 'Pythagorean' theorem to create his famous table of sine. Aryabhata discussed the concept of sine with the name ardha-jya which literally means 'half chord'. Some believe, that Aryabahata came up with the concept of sine when using a bow as the chord and arc he describes in his book Arabhatyia. Looking at the figure on the right, one can see the similarity between the figure and a bow.

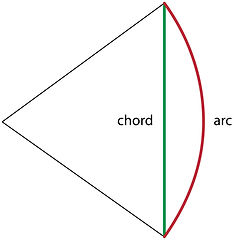
4ec788_d10c7d0006bb4820a70109081d36c609~

When Arabic writers translated his works from Sanskrit into Arabic, they referred to it as jiba. From there, in the 12th century, Gherando of Cremona translated these writings from Arabic to Latin and replaced the Arabic jaib with sinus, where the English word sine comes from. So if you've ever sat over a trigonometry problem at 2 am rethinking all your life choices, it's this guy's fault almost 1600 years ago.

tribhuj asya phalaśarīraṃ samadalakoṭī bhujārdhasaṃvargaḥ

 

This verse from Aryabhata's Ghantapada 6 states that "for a triangle, the result is perpendicular with half-side in the area"

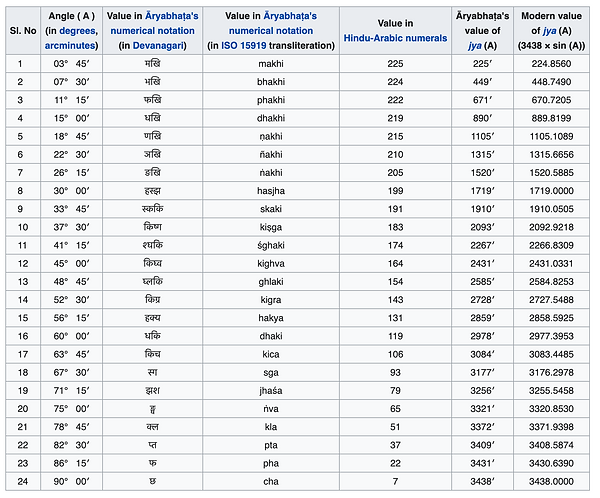
Aryabhata sine table compared to the modern version:

https://en.wikipedia.org/wiki/%C4%80ryabha%E1%B9%ADa%27s_sine_table#:~:text=The%20astronomical%20treatise%20%C4%80ryabha%E1%B9%AD%C4%ABya%20was,of%20arcs%20of%20a%20circle. Accessed 11 Jan 2021.

sine table.png

Just as you thought he could do no more, Aryabhata provides a vague explanation for quadratic equations, compound interest, proportions (ratios), compound interest, solutions of various linear equations. He also provides an obscure and incomprehensible general solution for linear indeterminate Diophantine equations, which Bhaskara I deciphered and called kuttaka ("pulverizer") consisted of breaking the problem down into new problems with successively smaller coefficients - essentially a precursor to Euclidean algorithm.

References:

  1. 1. Jacobs, Harold R. (2003). Geometry: Seeing, Doing, Understanding (Third ed.). New York: W.H. Freeman and Company. p. 70. ISBN0-7167-4361-2.

  2. Roger Cooke (1997). "The Mathematics of the Hindus". History of Mathematics: A Brief Course. Wiley-Interscience. ISBN0-471-18082-3

  3. Hayashi, Takao, "Aryabhata Biography And Facts". Encyclopedia Britannica, 2020, https://www.britannica.com/biography/Aryabhata- Accessed 6 Dec 2020.

  4. "Aryabhata". En.Wikipedia.Org, 2017, https://en.wikipedia.org/wiki/Aryabhata#cite_note-20. Accessed 6 Dec 2020.

  5. Ansari, S.M. Razaullah. “Aryabhata I, His Life and His Contributions.” Bulletin of the Astronomical Society of India, vol. 5, Mar. 1977, pp. 10–18., http://articles.adsabs.harvard.edu//full/1977BASI....5...10A/0000010.000.html.

  6. Victor J Katz (Editor) (2007). The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook. Princeton: Princeton University Press. pp. 405–408. ISBN978-0-691-114859.doi:

  7. "Āryabhaṭa's Sine Table". En.Wikipedia.Org, 2021, https://en.wikipedia.org/wiki/%C4%80ryabha%E1%B9%ADa%27s_sine_table#:~:text=The%20astronomical%20treatise%20%C4%80ryabha%E1%B9%AD%C4%ABya%20was,of%20arcs%20of%20a%20circle. Accessed 11 Jan 2021.

bottom of page