Madhava - 1350 to 1425 AD

Madhava of Sangamagrama an Indian mathematician and astronomer born in the 14th century were one of the greatest scholars of the middle ages; having made great contributions to the study of infinite series, calculus, trigonometry, geometry and algebra. A founder of the Kerala School of Astronomy and Mathematics, he cultivated a community of academics which is said to have influenced some European work.
In his text Yuktibhasa, Madhava discovered the infinite series for the trigonometric functions of sine, cosine, arctangent and several methods for calculating a circle's circumference. While the concept of deriving an infinite series may not seem like much of an accomplishment ("how hard can it be? just count forever" wise words said by my sister when I tried explaining the feat of this achievement). Infinite series are used in engineering, physics, computer science and finance to better understand basic concepts.
One of the series discovered by Madhava contains the derivation and proof of the power series for the inverse tangent, which was written by a student Jyesthadeva in this text which yields:
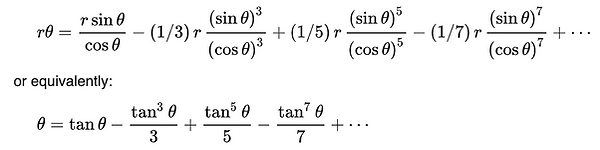
This series used to be called Gregory's series named after James Gregory who rediscovered this series 3 centuries after Madhava. So now, it's called the Madhava-Gregory-Leibniz series.
Madhava also composed an accurate table of sines (if you want to be a famous mathematician you know what you have to do ;) ). Marking a quarter circle with 24 arcs drawn at equal intervals in a quarter of a given circle. It is thought that he found these highly accurate tables was through the equivalent of these series expansions:

Madhava's work on Pi is cited in the Mahajyānayana prakāra ("Methods for the great sines"). The text explains the infinite series expansion of π now known as the Madhava-Leibniz series. The most impressive thing about it is that he gave a correction term, for the error after computing the sum up to n terms. He gave 3 expressions for the correction term. And the third correction leads to the highly accurate computation of π. It has been speculated that Madhava found these correction terms through a finite continued fraction.
Madhava also laid the foundations for the development of calculus, which has been credited to Newton and Leibniz (*casually sips tea*). But a team from the universities of Manchester and Exeter say that credit for this lies with the "Kerala school," "notably Madhava and Nilakantha". While not diminishing the contributions of these European scholars, the theory that Madhava's work influenced Europe cannot be disproven. As at the time, the port of Muziris, near Madhava's dwelling was a major centre of maritime trade and scholars, such as G. Joseph of the U. Manchester have suggested that the writings of the Kerala school may have also been transmitted to Europe around this time, a century before Newton.
References:
-
J J O'Connor and E F Robertson, "Madhava - Biography". Maths History, 2021, https://mathshistory.st-andrews.ac.uk/Biographies/Madhava/. Accessed 17 Jan 2021.
-
"Madhava Of Sangamagrama". En.Wikipedia.Org, 2021, https://en.wikipedia.org/wiki/Madhava_of_Sangamagrama#cite_note-predated-27. Accessed 17 Jan 2021.
-
"Calculus Created In India 250 Years Before Newton: Study | CBC News". CBC, 2016, https://www.cbc.ca/news/technology/calculus-created-in-india-250-years-before-newton-study- 1.632433#:~:text=Researchers%20in%20England%20may%20have,end%20of%20the%20seventeenth%20century. Accessed 17 Jan 2021. But that's just to get the 3 minutes mark
-
C. K. Raju (2007). Cultural foundations of mathematics: the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE. Delhi: Pearson Longman. There's a lot more information here.
